Coordinate System Exercises [2/11]
Coordinate System Exercises
First, run the accompanying demonstrational program. Demonstrational programs are not explained in detail.
This program draws a growing disc. At the start of the program, the center of the disc is at the middle of the screen, but you can move the disc around by using a mouse or touch.
The position of the disc's center is given by the coordinates x and y. The program makes the coordinates change as you move the mouse around. The disc and the accompanying items are then redrawn according to the position given by the coordinates x and y.
- The x coordinate specifies the distance from the left side of the screen.
- The y coordinate specifies the distance from the top of the screen.
The radius is the distance from the disc center to the disc edge. The radius equals half the disc size. The disc size is called the diameter. The diameter always equals twice the radius.
Exercise:
Use this program to find out the maximum x and y coordinates. The maximum coordinates describe the size of the output image.
Solution
The size of the output screen can be figured out by holding down the left mouse button while the program is running and moving the mouse into the bottom-right corner of the screen. The maximum x-coordinate equals 960; the maximum y-coordinate equals 720.
Click on the 'Next' button (at the top of the page) to proceed.
The given program draws a disc touching the left edge of the screen.
The disc touches the left edge of the screen because the radius is equal to the x coordinate.

Exercise 1: Draw a disc touching the top edge of the screen, of the color azure with a radius of 90 pixels.
Note: Sometimes there can be multiple correct answers, so the provided solution may not match exactly with your solution.
Solution 1
disc(480, 90, 90, /azure);

Exercise 2: Draw a disc touching the bottom edge of the screen, of the color pink with a radius of 90 pixels.
Solution 2
disc(480, 720-90, 90, /pink);

Exercise 3: Draw a disc touching the right edge of the screen, of the color gold with a radius of 90 pixels.
Solution 3
disc(960-90, 200, 90, /gold);
This program draws two intersecting lines.
The line function has the form:
line(x1, y1, x2, y2, color)
Exercise 1: The cyan line lies entirely on the same x coordinate. What is the value of x coordinate for the entire cyan line?
Solution 1
The x coordinate of the entire cyan line equals 340.
Exercise 2: The yellow line lies entirely on the same y coordinate. What is the value of y coordinate for the entire yellow line?
Solution 2
The y coordinate of the entire yellow line equals 410.
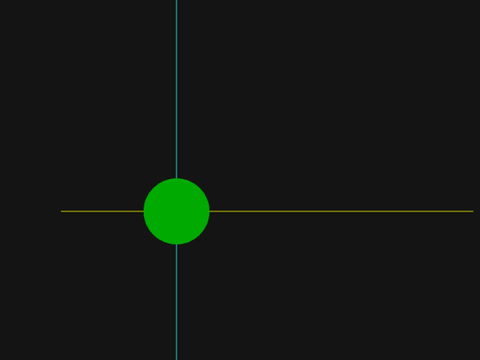
Exercise 3: Draw a green disc centered at the intersection of the lines. The radius should be 40 pixels.
Solution 3
disc(340, 410, 40, /green);
This program draws a green disc.

Exercise 1: Draw a vertical cyan line through the center of the green disc.
Solution 1
line(400, 0, 400, 720, /cyan);
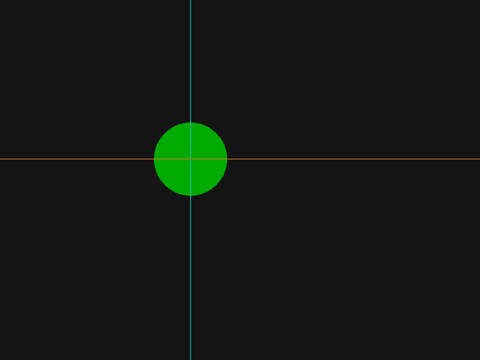
Exercise 2: Draw a horizontal orange line through the center of the green disc.
Solution 2
line(0, 300, 960, 300, /orange);
This program draws three lines.
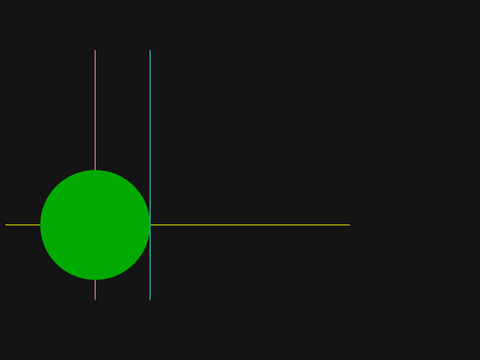
Exercise: Draw a green disc centered on the intersection of the pink and the yellow line, also, the disc should touch the cyan line
Hint 1
First, you need to figure out what values should be assigned to the x and y coordinates of the green disc center.
Hint 2
The x coordinate of the green disc center must be equal to the distance from the pink line to the left side of the screen. Write this number down.
Hint 3
The y coordinate of the green disc center must be equal to the distance from the yellow line to the top of the screen. Write this number down.
Hint 4
Finally, you must figure out what should be the radius of the green disc.
Hint 5
The radius of the green disc must be equal to the distance between the pink line and the cyan line. Write this number down.
Solution
disc(190, 450, 300-190, /green);
This program draws two lines.
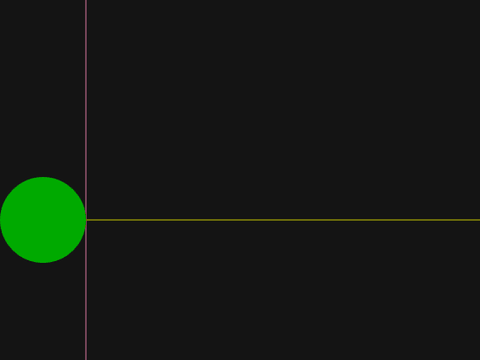
Exercise: Draw a green disc that has a center on the yellow line; also, the disc should be touching the pink line and the left edge of the screen.
Hint 1
What is the distance between the pink line and the left edge of the screen?
Answer
The distance between the pink line and the left edge of the screen equals 180 pixels because the entire pink line lies on the x coordinate equal to 180. The x coordinate always equals the distance from the left edge of the screen.
Hint 2
What should the radius of the green disc be equal to?
Answer
The radius of the green disc should be 90 pixels, which means that the size (diameter) of the disc equals 180 pixels.
Hint 3
The x coordinate of the green disc center must equal the radius, and the y coordinate is given by the yellow line.
Solution
disc( 90, 450, 90, /green);
This program draws one pink line.

Exercise: Draw a green disc touching the top edge of the screen, the left edge of the screen and the pink line.
Solution
disc(120, 120, 120, /green);
This program draws a red disc and a green disc.
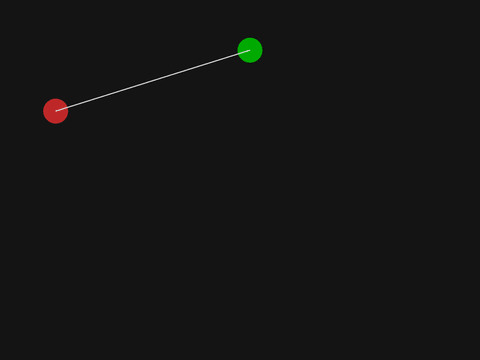
Exercise: Connect the red disc and the green disc with a white line.
Solution
line(111, 222, 500, 100, /white);
This program draws a red disc and a line of blue discs.
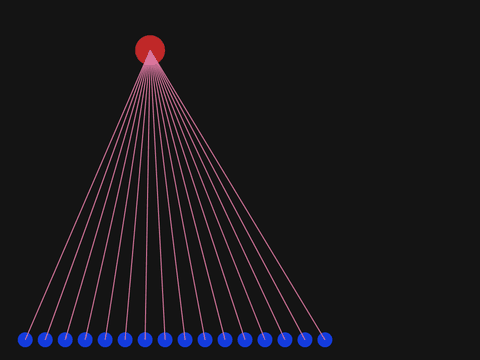
Exercise: Draw pink lines connecting the center of the red disc with each of the blue discs.
If you can't solve this exercise, take a peek at the solution. You don't need to solve every exercise by yourself. A lot can be learned by simply reading the solution and applying it.
Solution
Insert this statement before the sleepMs statement:
line(300, 100, i, 680, /pink);
We can now draw an image resembling a sunrise by using three for loops.
The step of the first for loop equals -7, and the initial value is greater than the bounding value.
The fillScr function fills the entire screen with the given color.
This program draws a line of green discs. The center of the first disc is at the left edge of the screen. The discs are drawn from left to right.
Exercise:

Change the program so that the first disc is centered at the right edge of the screen. The discs should be drawn from right to left.
There are two ways to solve this problem, and you should try both. The first solution involves changing only the first line of the program. All three values of the for loop must be changed: the initial value, the bounding value and the step of loop. The step can be a negative value.
Solution
for #x = 960 .. 500 -=100
The second solution involves changing the coordinates of the disc function. First, you should reset the program to its original state by reloading this page. You can reload the page either by pressing the F5 key, by pressing the Ctrl-R key combination, or by clicking on the reload button of your browser.
In this second solution, you are only allowed to modify the call of the disc function.
Hint 1
Only the first argument of the disc function should be modified.
Hint 2
A subtraction operation needs to be performed.
Solution
disc(960-x, 300, 50, /green);
Click on the 'Articles' button at the top to select another article. We also suggest taking a peak into our main 'Gallery' of programs, and taking a look into 'Overview' of our main programming tutorial for beginners. Have fun!
<< F2:Prev - - F4:Next >>