Simple Graphics [1/15]
Simple Graphics
This program draws multiple white circles.
The circles have a radius of 15.
[Run the program]
The circle procedure is used to draw circles.
Its form is:
circle(x, y, radius)
There are two calls to the circle procedure in the loop's body.
Procedure calls can be easily recognized because they must use parentheses to enclose the arguments. Each procedure call is made in a separate statement.
Exercises:
Change the radius to 25 in the first row of circles.
[Run the program]Change the radius to 30 in the second row of circles.
- Track your progress by clicking the “Overview” button at the top left menu.
- Take regular breaks to stay focused and refreshed.
The given program contains an error.
The error report may not be very helpful, as the automatic verifier can't always identify the exact problem.
Challenging exercises are a crucial part of learning. They provide valuable learning experiences, even if they're difficult.
Exercise:
1. Try to correct the error.
Inside an expression, a symbol / denotes division. Therefore, 20 /darkorange means “20 divided by darkorange”, which does not make sense.
If the exercise is too challenging, it's okay to look at the solution. First, try to solve it on your own, and if needed, consider reading the hint for additional guidance.
Hint
Arguments must be separated by a comma (,).
Solution
disc(x, 200, 20, /darkorange);
[Run the program]
2. Insert the statement
println "x: ", x;
just above the disc procedure call,
inside the loop's body, within { } .
[Run the program]
The step of the for loop is -50,
and the initial value (800) is greater than the bounding value (100).
This causes the discs to be drawn from right to left.
[Run the program]
Exercises:
Insert the statement println "x: ", x; just above the disc procedure call, inside the loop's body.
[Run the program]Change the argument of the sleepMs procedure call to value 500.
[Run the program]Increase the spacing between the discs.
After solving an exercise, it's a good idea to review it by comparing to the the provided solution.
Note that there may be multiple correct solutions, so the provided solution might not match exactly with your solution.
Solution
for #x=800..100 -=75
This program is for demonstration purposes only.
[Run the program]
Important:
Do not analyze this program in detail,
as it contains features that will be explained later.
This program visualizes the screen's coordinate system.
The x-coordinate increases to the right, and the y-coordinate increases downwards. Coordinates are written as a pair (x,y).
The top left corner of the screen is at coordinates (0,0).
This program draws four red discs.
[Run the program]
The text after symbols << is a comment. Comments are ignored by the computer.
The program makes four calls to the disc procedure.
The disc procedure accepts four arguments: disc(x, y, radius, color)
Exercise 1:

Draw a yellow disc in the middle of the red discs. It should touch all four red discs.
Solution
Append this statement to the program:
disc(500, 400, 50, /yellow);
Exercise 2:

Draw a green disc touching the rightmost red disc from the right side.
Solution
disc(700, 400, 50, /green);
The program starts with a multiline comment, which begins with /* and ends with */. The computer ignores the contents of multiline comments.
To draw a vertical line of discs, the second coordinate (commonly named y ) of the disc procedure call is changing.
Exercises:
1. Change the first argument (300) in the call to disc procedure. Try several values between 0 and 700.
2. Swap over the first and the second argument in the call to disc procedure. What effect will this have?
Solution
disc(y, 300, 20, /red);
3. Rename the variable y to x in both places. What difference will that make? Verify your answer by clicking on the box below.
Answer
After solving an exercise, it is recommended that you always examine the provided solution.
The fillScr procedure fills the entire screen with the given color.
The disc procedure has an optional fourth argument: color. If omitted, the disc is painted in the current global foreground color, which is initially white.
Note: In each of the exercises, make sure to include any changes made in the previous exercises, as each exercise builds upon the previous ones. When you have completed an exercise, always run the program to see the results.
Exercises:
Change the program so that the disc is painted in the green color.
Solution
disc(480, 360, i*5, /green);
Insert this statement just below the fillScr statement: println "This program draws a growing disc";
Insert this statement just above the disc statement: println "One iteration executed";
Insert this statement at the beginning of the loop's body: fillScr(/violet);
Change the println statement in the for loop to also print the value of variable i in each iteration.
Solution
println "One iteration executed, ", i;
The line procedure draws a line. It can accept five arguments: line(x1, y1, x2, y2, color)
Arguments are sometimes also called parameters. The last parameter, color, can be omitted.
This program contains two calls of the disc procedure, and one call of the line procedure. A procedure call causes the execution of the procedure.
Exercises
1. Modify the second call of procedure disc to draw at coordinates (555, 444).
2. Modify the call of procedure line so that it connects the two discs.
Solution
line(70, 90, 555, 444, /yellow);
This program draws three discs and one line.
[Run the program]
Single-line comments can also be written after symbols /// . This type of comment is the same as the one after symbols << .
Exercise 1

Draw a line connecting the red disc and the purple disc.
Solution
line(300, 200, 300, 500);
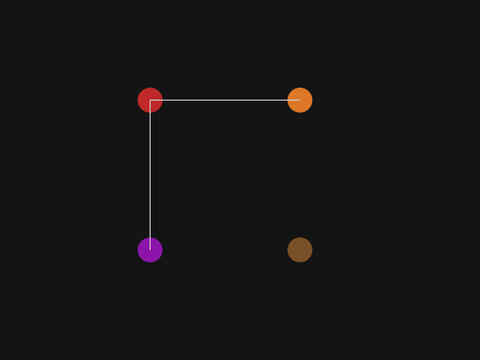
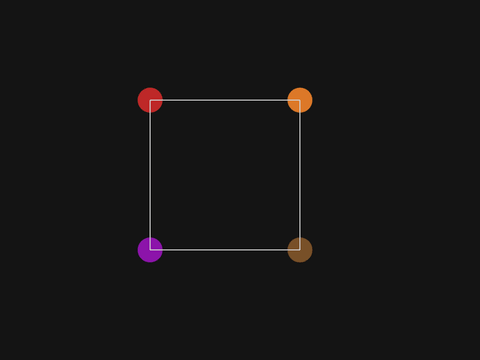
Exercise 2
Draw a brown disc so that the discs form a square.
Solution
disc(600, 500, 20, /brown);
Exercise 3
Draw the remaining two sides of the square.
Solution
line(300, 500, 600, 500); line(600, 200, 600, 500);
This program draws four discs and three lines.
[Run the program]
Exercise
1. Add a line connecting the fourth disc and the bottom point of the other lines.
Solution
line(480, 200, 350, 440);
In this example, a for loop is used to draw a series of lines that form a triangle.
An unusual pattern should be slightly visible, especially near the bottom of the triangle.
This pattern is called moiré (mwoa-RAY).
[Run the program]
Experiment with different step values (the number 9) in the for loop to see how they affect the moire pattern. Try values like 3, 4, 6, or 12.
The linep procedure has the form:
linep( [pointA], [pointB] )
Exercises:
The disc procedure has the form:
disc(x, y, radius, color)
1. Draw an orange disc of radius 20 at the bottom point of the triangle.
Solution
disc(450, 650, 20, /orange);
2. Change the step of the loop to 30.
3. Inside the body of the for loop, add a red disc of radius 15 at the top end of each line.
Solution
disc(i, 100, 15, /red);
This program draws a red disc and a row of yellow discs.
[Run the program]
Exercise:
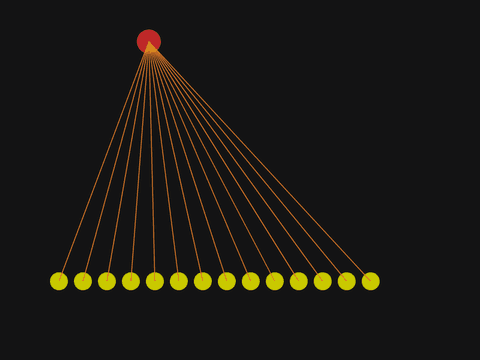
Draw orange lines connecting the center of the red disc with each of the yellow discs.
Hint: Inside the body of the for loop, insert a new call of procedure line above the sleepMs call. The line procedure accepts five arguments. The first two arguments are coordinates of one line endpoint. The next two arguments are coordinates of the other line endpoint. The final, fifth argument is the line color.
If you get stuck, you can take a look at the solution. You don't need to solve every exercise on your own, and you can learn a lot by reading and understanding the solution.
Hint 2
Use the disc center coordinates from the program's source code as the line endpoints.
Solution
Insert this statement above the call to sleepMs:
line(300, 100, i, 500, /orange);
This program draws two lines of discs simultaneously.
The discs are 50 pixels apart.
[Run the program]
Exercise:
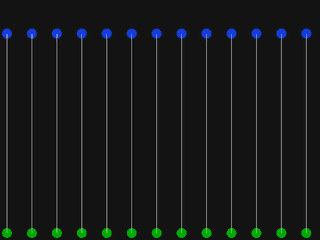
Draw lines connecting the centers of disc pairs.
If you need help, then examine the hints carefully one by one. If you're still having trouble, take a look at the solution.
Hint 1
Since the lines connect disc centers, use the same coordinates for the line procedure call as for the corresponding disc procedure calls.
Hint 2
The disc procedure has the form:
disc(x, y, radius, color)
The line procedure has the form:
line(x1, y1, x2, y2)
Solution
Just above the call to sleepMs, insert: line(i, 100, i, 700);
This program draws a bunch of lines.
The top line ends move rightward, while the bottom line ends move leftward.
[Run the program]
The third argument of the line procedure call is 960-i. It causes the bottom line ends to move leftward as i increases.
To accomplish the movemement leftward, a subtraction operation was performed in the third argument of the line procedure call.
Exercise:
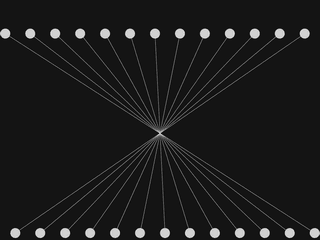
Draw discs at the ends of each line. The radius should be 10 pixels.
Hint 1
Since the lines connect disc centers, use the same coordinates in the disc procedure calls as the corresponding coordinates in the line procedure call.
Hint 2
The disc procedure has the form:
disc(x, y, radius)
The line procedure has the form:
line(x1, y1, x2, y2)
Solution
Just above the call to sleepMs, insert: disc(i, 100, 10); disc(960-i, 700, 10);
This program draws a triangle consisting of spaced lines,
creating a slight moiré pattern (mwoa-RAY pattern).
[Run the program]
Exercises:
1. What happens when you change the last argument (the number 650) of the line procedure call? Try out different values, such as 400, 200, 0, and 500.
2. What happens when you change the second argument of the line procedure call? Try out different values between 0 and 700.

3. Change the program so that the triangle of lines is displayed upside-down.
Solution
line(450, 650, x, 100);
<< F2:Prev - - F4:Next >>